반응형

이진 탐색(Binary Search)
이진 탐색은 지정한 데이터 값을 리스트, 배열과 같은 데이터 집합에서 탐색하기 위한 알고리즘입니다.
집합에서 탐색 범위를 이분해 좁혀가며 지정한 데이터 값을 탐색합니다.
특징
- 배열 내부의 데이터가 정렬되어 있어야만 사용할 수 있습니다.
정렬 알고리즘은 이전 포스팅을 참고해 주세요!
[알고리즘] 삽입 정렬(Insertion Sort)
Table of Contents 함께보면 좋을 포스팅 [알고리즘] 선택 정렬(Selection Sort) Table of Contents 선택 정렬의 이해 방식 선택 정렬은 크게 3단계로 동작합니다. 지정 : 정렬 후 원소를 집어넣을 위치(인덱스)
doinitright.tistory.com
작동 방식
- 데이터 탐색을 위해 집합에서 탐색할 범위를 설정하는 변수 3개를 지정합니다. `(처음, 끝, 중간)`
- `처음 (start)` : 처음 인덱스
- `끝 (end)` : 끝 인덱스
- `중간 (mid)` : 처음과 끝의 중간지점 인덱스, `처음 + 끝 / 2`
- 중간의 값이 탐색한 값보다 작거나 / 크거나 에 따라 처음, 끝, 중간 변수의 위치를 옮겨가며 반복 탐색합니다.
- 탐색 1회전마다 탐색할 범위를 이분하여 줄여나갈 수 있습니다.
- `중간 값 < 탐색 값` : `start` 인덱스를 중간 값 + 1로 이동
- '중간 값 > 탐색 값' : 'end' 인덱스를 중간 값 -1로 이동
- '중간 값 == 탐색 값' : 탐색 완료
- 이후에는 'mid' 인덱스를 start 혹은 end 인덱스의 이동에 따라 재설정합니다. `처음 + 끝 / 2`
- 탐색 1회전마다 탐색할 범위를 이분하여 줄여나갈 수 있습니다.
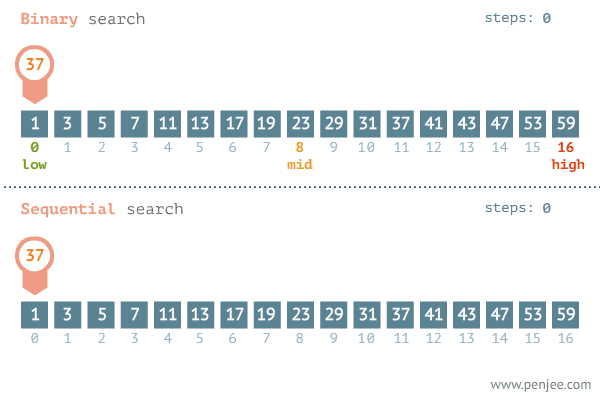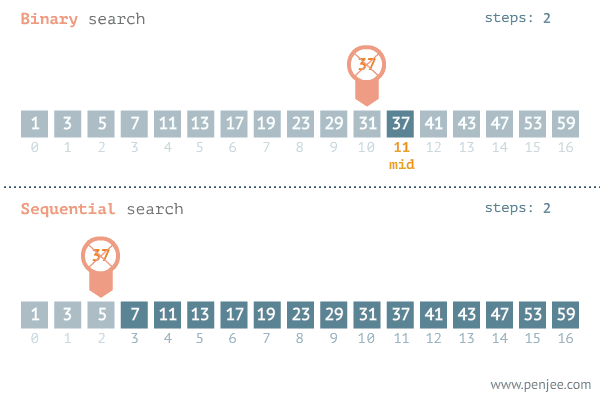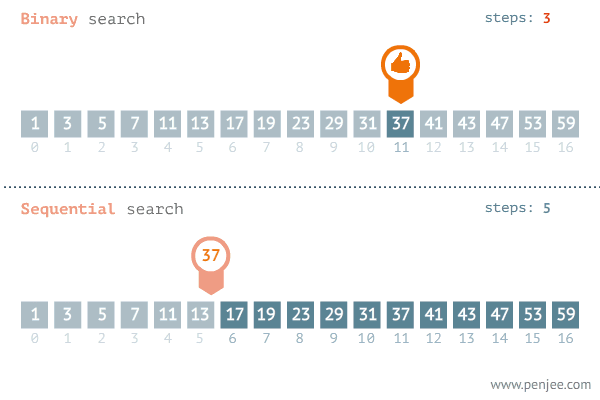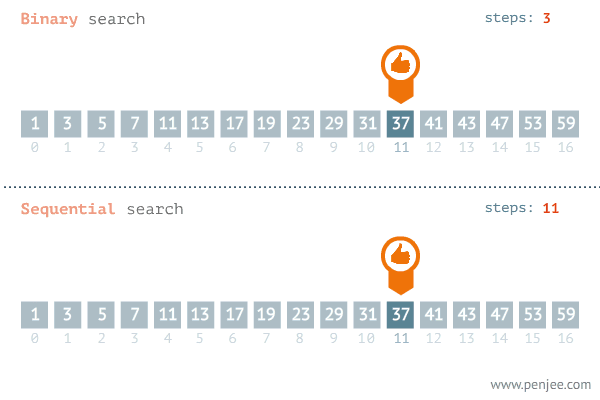
시간복잡도 vs 순차 탐색
순차 탐색의 시간복잡도 : `O(n)`
이진 검색의 시간복잡도 : `O(logn)`
이진 탐색은 탐색이 반복될 때마다 탐색 범위가 절반씩 감소하며, 값을 찾을 확률이 배가 됩니다.
구현 코드(java)
Q. 정렬된 배열 `arr` 이 주어질 시 주어진 목푯값 `m` 이 `arr` 의 몇 번째에 위치해 있는지 구한다.
EX. `arr = {1, 2, 3, 5, 6}`, `m = 5` → 정답 : 4
while문을 활용한 이진 탐색 알고리즘 메서드 구현
public int method(int m, int[] arr) { // m : 탐색 목표 값, arr : 탐색할 배열
// 탐색 목표값의 위치를 저장
int answer = 0;
// 탐색 범위를 설정하는 start, end
// [초기값] start : 배열의 첫 인덱스, end : 배열의 끝 인덱스
int start = 0, end = arr.length - 1;
while(start <= end){
// 1회전마다 변화된 start, end 에 따른 중간 값 재설정
int mid = (start + end) / 2;
// 중간 값 == 목표 값 (탐색 성공)
if (arr[mid] == m) {
answer = mid + 1; // index + 1번째에 있으므로 1을 더한다
break;
}
// 중간 값 != 목표값 (start, end 인덱스 이동해 탐색 범위 이분)
else if (arr[mid] > m) end = mid - 1;
else start = mid + 1;
}
return answer;
}
핵심은 2가지입니다.
- 중간값을 가리키는 `mid` 인덱스를 통해 탐색 목푯 값과 비교하는 것
- 비교 결과에 따라 `start, end, mid` 인덱스를 재설정하며 탐색 범위를 줄여가는 것
예제 실행 결과
public static void main(String[] args) {
BinarySearch bs = new BinarySearch();
int[] arr = {1, 2, 3, 5, 6};
int m = 5;
System.out.println(bs.method(m, arr));
// out : 4
}
# 구현 코드
반응형
'DEV > Algorithm' 카테고리의 다른 글
| [java][알고리즘] 비트마스크(Bit Mask)를 통한 배열의 부분집합 구하기 (0) | 2023.11.13 |
|---|---|
| [알고리즘] [java] 피보나치 수열과 메모이제이션 (1) | 2023.10.29 |
| [java, 알고리즘] 삽입 정렬(Insertion Sort) (2) | 2023.10.10 |
| [java, 알고리즘] 버블 정렬(Bubble Sort) (0) | 2023.10.09 |
| [java, 알고리즘] 선택 정렬(Selection Sort) (0) | 2023.10.09 |